
Basics of Harmonic Distortions (Part 1)
The load current of a purely resistive load is sinusoidal and in phase with the voltage. When the load also contains reactance, a phase-shift between the voltage and current is introduced. However, the current waveform is still sinusoidal. Loads that draw sinusoidal current are called linear loads.
A load is considered non-linear if the current it draws from the supply is not sinusoidal. In other words, the current the load draws changes non-linearly with respect to supply voltage. Non-linear AC current is usually caused by rectification of the AC current for DC loads or for frequency converters. Modern networks comprise a large variety of non-linear loads. Some common examples are computers, mobile phone chargers, modern LED and fluorescent lighting, UPS systems and variable speed drives in industrial environments. An example of voltage and current waveform of a three-phase diode rectifier is depicted in Figure 1.
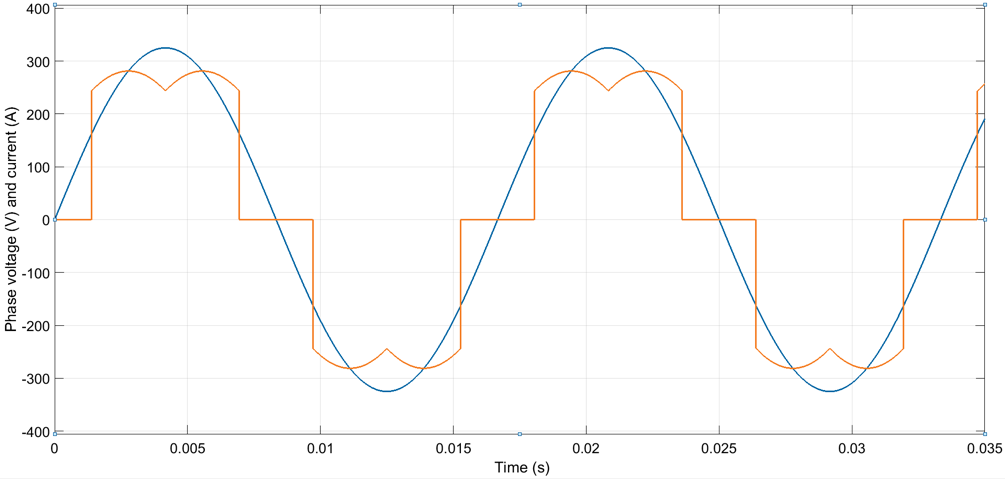
Figure 1: Typical current waveform of a rectifier.
Though highly distorted current waveforms may not resemble a sine wave even distinctly, all arbitrary waveforms can be constructed from a sum of sine waves of different frequencies and amplitudes by using Fourier analysis. These components of different frequencies are called harmonic components or harmonics. Harmonic components are numbered by multiples of fundamental frequency; in 50 Hz system 3rd harmonic component corresponds to the harmonic of frequency 150 Hz = 3×50 Hz, 5th harmonic component corresponds to the harmonic of frequency 250 Hz = 5×50 Hz etc.
Figure 2 presents two periods of a distorted current waveform including fundamental frequency component and the 3rd, the 5th and the 7th harmonic components. The same resultant current is then separated into its sinusoidal components in Figure 3.
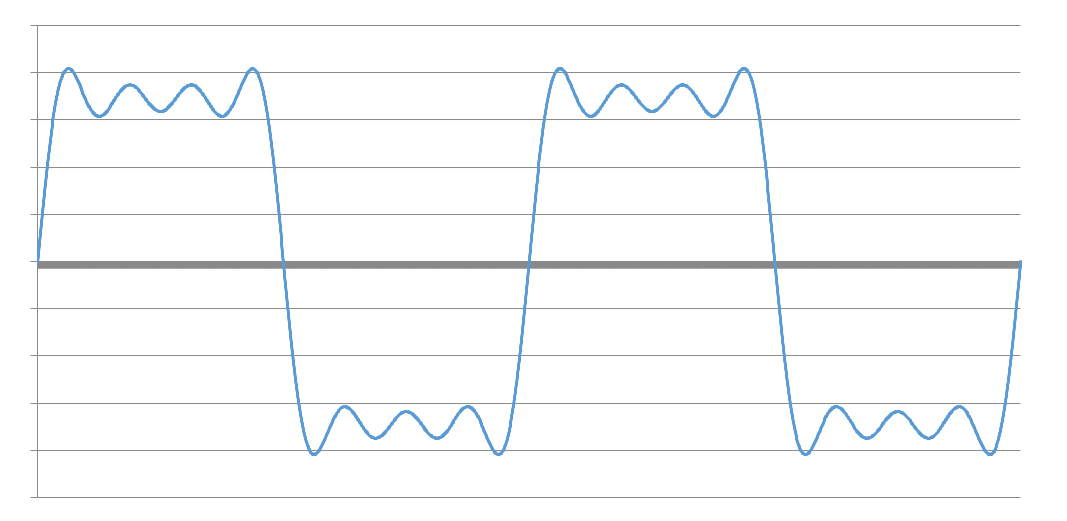
Figure 2: Current waveform comprising of the fundamental current and the 3rd, 5th and 7th harmonic currents.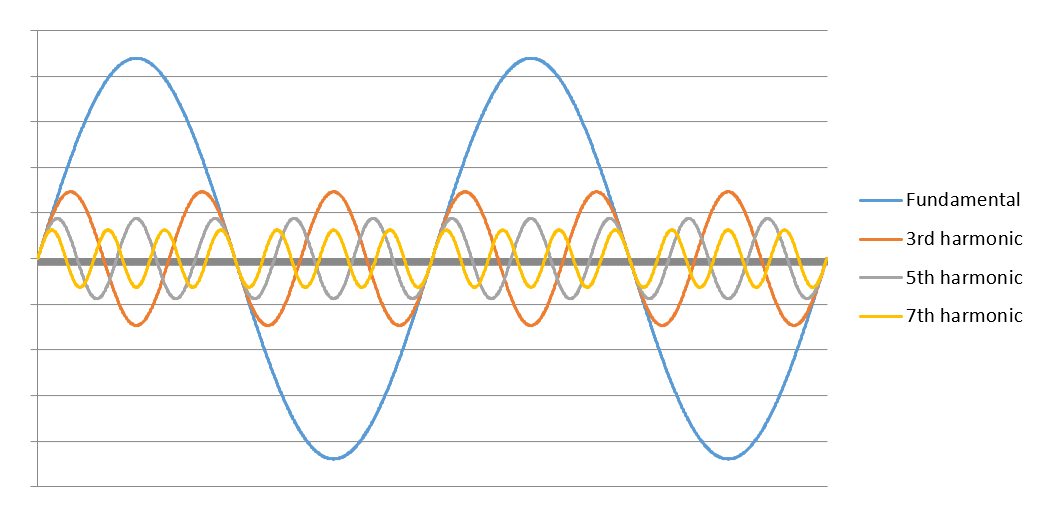
Figure 3: Current components of the current waveform shown in Figure 2.
From Figure 3 can be seen that the third harmonic current indeed goes through exactly three periodic sequences in the same amount of time that the fundamental frequency goes through only one sequence