Blog

What are the benefits of improving power factor? (Part 1)

Electricity transmission and distribution systems are designed to carry a certain amount of current without overloading. Too much current causes excessive resistive losses in electric elements and can result in overheating and excessive voltage drop. If the reactive power of a load with poor power factor is not compensated locally, the reactive power needs to be supplied from the power source.

To maximize the capacity of the electric network, transfer of reactive power should be kept at the minimum. Utilities require certain level of DPF from power users and may penalize for excessive reactive power transfer from the power source. The increase in active power transmission capacity with the existing transmission and distribution system by local reactive power compensation is explained in figure 1.

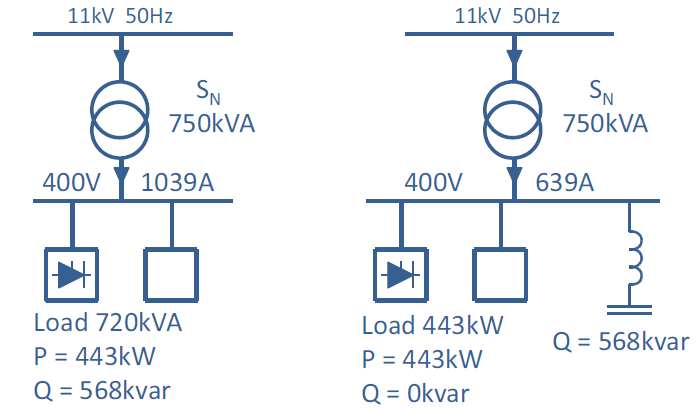
Figure 1: Active power supply capacity is increased when reactive power is compensated locally.

Since the nominal capacity of the transformer in figure 1 is 750 kVA, and no reactive power needs to be transmitted from the supplying network when local compensation is used, the whole capacity of the transformer can be used for active power supply. Thus, the increase in active power supply capacity in the case of figure 1 would be 750 kW – 443 kW = 307 kW. The increase in transmission capacity with respect to power factor improvement is presented graphically in figure 2.

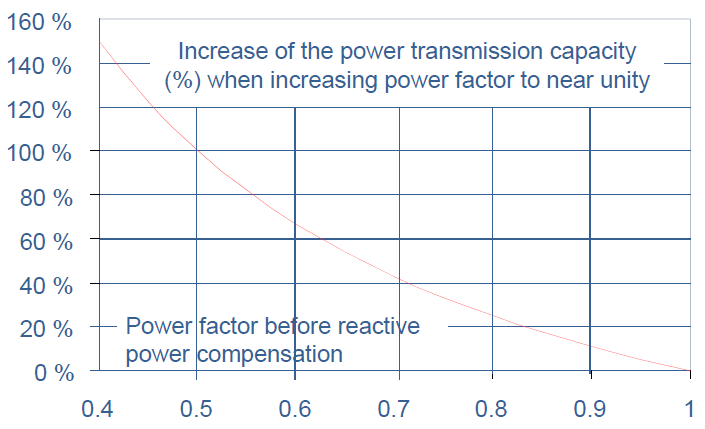
Figure 2: Increase in power transmission capacity with increased power factor.

The load current floating through the transmission and distribution system causes power losses and voltage drop in the impedances of the network components. The phase to neutral voltage drop caused by active and reactive current is roughly

Where R is the resistance of the network and X is the reactance of the network. Since the ratio R/X is usually between 0.1 and 0.2, the voltage drop is mainly caused by the transmission of reactive current. Voltage support by reactive power compensation can be estimated with equation (6):

Where Q_C is the capacitor reactive power and S_K is the short circuit level of the network at the point of compensation. In figure 8 is presented an example network supplying a 50 MW load with power factor of 0.75. This gives 44.1 MVAr of reactive load.

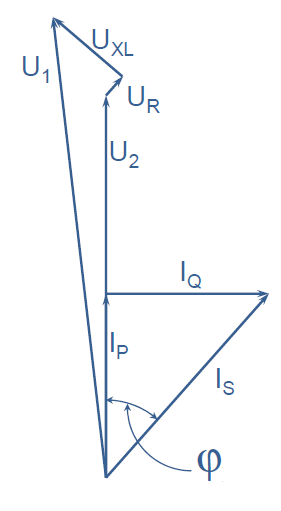
Figure 3: Voltage drop caused by transmission of active and reactive current through network impedances when reactive power is not compensated.

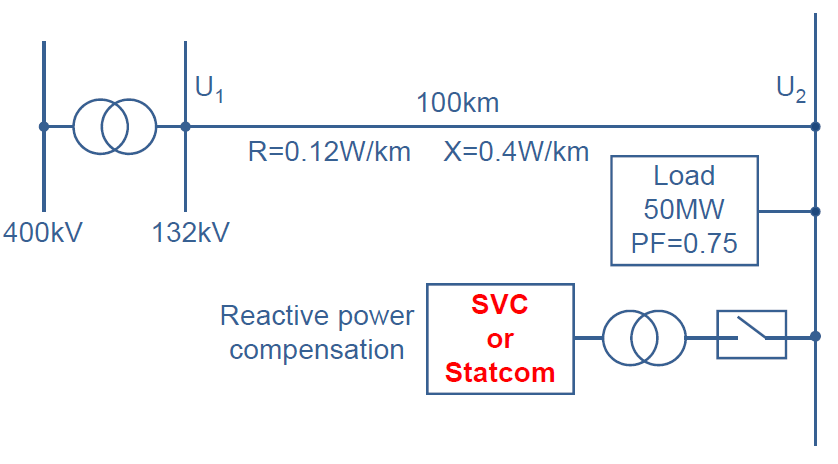
Figure 4: Transmission network supplying load with poor power factor.

In figure 3 are presented the voltages U₁ and U₂ and the losses caused by the transmission of active and reactive power through the transmission line when the reactive power compensation equipment presented in figure 4 is not in use.